После прочтения книги «Три дня в Карликании» [1] захотелось найти как можно больше разных систем счисления. Это так интересно увидеть и понять, как в древности люди писали цифры, какие для этого они применяли значки. Как из этих цифр они составляли числа. Для этого был проведен поиск литературы, как в библиотеке, так и в Интернете.

Много интересного о разных системах нумерации на сайте «Всевозможные нумерации и системы счисления» [3]. Подробно о древних цифрах и числах можно найти в книгах [3-5]. История нуля рассказана в статье «Триединый нуль» [6]. Очень трудно найти подробное описание нумерации чисел индийцев Майа, но в книге «Тайна жрецов майя» [7] она приведена.

2 Цифры и системы счисления

2.1 Зачем числа?

"Все есть число", — говорили пифагорийцы (ученики древнегреческого математика Пифагора). Значит всё можно обозначить числом.

Так как многие предметы внешнего мира имеет схожую форму, возникла потребность их сосчитать. Например, сколько коров в стаде. Сколько добыто рыб, или зайцев. Т.е. число и арифметика возникли из практической деятельности человека.

Так как многие народы в древности не общались друг другом, то у разных народов возникли разные системы счисления и представления чисел и цифр.

Число - это обобщение, так как разными числами можно подсчитать разные предметы.

Цифры – это значки, с помощью которых записывают числа. Система счисления или нумерация – это способ записи чисел с помощью цифр.

2.2 Простая система счисления

У первобытных людей не было даже чисел, они количество предметов отображали равным количеством каких-либо значков. Такими значками могли быть зарубки, черточки, точки, а так же узелки на веревках.

Это самая простая система счисления. В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки ½, кружочка ○, или любой другой фигуры. Тогда числа будут записываться примерно так:

1	½
2	½½
3	½½½
4	½½½
5	½ ½ ½ ½ ½ и т. д.

Такая система счисления использовалась, и до сих пор используется народами, не имеющими письменности.

Но иногда такой системой счисления пользуются и современные люди, например, отмечая зарубками количество прошедших дней, или карандашом отмечая черточками в тетради количество проданных товаров.

Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.

Но это удобно, пока числа небольшие. Вы только представьте себе число 1 000 записанное с помощью кучки камушков, а 1 000 000? Неудобно?

И люди начали изобретать системы счисления.

2.3 Позиционные и непозиционные системы счисления

Системы счисления бывают непозиционными (аддитивными) и позиционными (мультипликативными).

Чтобы разобраться в этом рассмотрим для примера нашу «арабскую» систему счисления. Например, число 3333 – три тысячи триста тридцать три. Здесь каждая цифра «3» в зависимости от того, в каком месте находиться обозначает свое число. Первая тройка слева, это три тысячи, вторая, три сотни, третья – три десятка, четвертая – три единицы. Т.е. это позиционная система. В таких же системах значение каждой цифры, зависит от ее положения (места, позиции) в записи числа. В непозиционных системах значение каждой цифры не зависит от ее положения (места, позиции) в записи числа.

Число 3333 можно представить в таком виде 3×1000 + 3×100 + 3×10 + 3. Т.е. для представления этого числа используется умножение (по-английски multiplication), отсюда название этой системы - мультипликативная.

В непозиционных же системах для представления числа используется сложение всех цифр, по-английски сложение – add. Поэтому другое название этих систем - аддитивные.

2.4 Основание системы счисления

Основание системы счисления – это число, на основе которого ведется счет. Например, если основание системы счисления равно десяти, то минимальная счетная группа этой системы счисления равна десяти, это значит, что, сосчитав какие-либо предметы до десяти, мы считаем снова с единицы, но при этом запоминаем число десятков. В нашей «арабской» системе основанием является число десять. Есть системы счисления и с другим основанием. Это такие системы счисления как пятеричная, двенадцатеричная, двадцатеричная, шестидесятеричная.

Десятеричная и пятеричная система возникла от того факта, что на одной руке человека пять пальцев, на обоих руках 10 пальцев.

Так проще считать. Если добавить пальцы и на ногах, то будет понятная и двадцатеричная система. Происхождение двенадцатеричной системы тоже связано со счетом на пальцах. Считали большой палец руки и фаланги остальных четырех пальцев.

Если двенадцать умножить на пять получим шестидесятеричную систему. Например, на одной руке загибаем пальцы, пока не получим, что отсчитано, пять штук, а на другой руке прикосновением большого пальца к суставам остальных четырех указываем количество этих пятерок.

В некоторых системах счисления используются для обозначения цифр буквы, такие системы счисления называются алфавитными.

Итак, бывают непозиционные (аддитивные) и позиционные (мультипликативные), пятеричные, десятичные, двенадцатеричные, двадцатеричные, шестидесятеричные и алфавитные системы счисления.

Вначале рассмотрим непозиционные (аддитивные) системы счисления.

3 Непозиционные системы счисления

3.1 Древнеегипетская десятичная

Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.

Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной и аддитивной.

	1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки.
	Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем ряду должно быть столько же палочек, сколько и в верхнем, или на одну больше.
	10. Такими путами египтяне связывали коров
	Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.
	100. Это мерная веревка, которой измеряли земельные участки после разлива Нила.
	1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка.
	10 000. "В больших числах будь внимателен!" - говорит поднятый вверх указательный палец.
	100 000. Это головастик. Обычный лягушачий головастик.
	1 000 000. Увидев такое число, обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф
	10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца

Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.

- 1205, - 1 023 029

Попробуйте сложить эти два числа, зная, что более 9 одинаковых иероглифов использовать нельзя, и вы сразу поймете, что для работы с этой системой нужен специальный человек. Обычному человеку это не под силу.

3.2 Римская пятеричная

Это, наверное, самая известная система, после «арабской», она возникла более двух с половиной тысяч лет назад в Древнем Риме.

I	1
V	5
X	10
L	50
C	100
D	500
M	1 000

Предполагаемое происхождение римских цифр

Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Например, XI = 11, XII = 12, XIII = 13, но следующее число уже особенное, так как такое число «XIIII» писать не удобно, римляне придумали сокращения, они стали писать так XIV = 14, т.е. 10+5-1 = 14. Т.е. если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание. Так же записывалось число 9 = IX. И кроме этого нельзя было писать четыре одинаковые цифры подряд, например, «XXXX» = XL (50-10) = 40.

О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (скорее всего этрусков). Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы - до XVI века.

В Санкт- Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника.

Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д.

3.3 Древнегреческая аттическая пятеричная

В древнейшее время в Греции была распространена так называемая Аттическая система счисления, название происходит от области Греции – Аттики со столицей Афины.

В этой системе числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок: ,,,. Число 5 записывалось знаком (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:

Число 10 обозначалось - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:

Числа в пределах первого десятка тысяч записывались так:

3.4 Древнегреческая ионийская десятеричная алфавитная

Примерно в третьем веке до нашей эры аттическая система счисления в Греции была вытеснена другой, так называемой "Ионийской" системой (она возникла в Милеете – греческая малоазиатская колония Ионии). В ней числа 1 - 9 обозначаются первыми буквами древнегреческого алфавита:

числа 10, 20, … 90 изображались следующими девятью буквами:

числа 100, 200, … 900 последними девятью буквами:

Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше.

Для отличия цифр и букв писали черточки над цифрами.

Древние евреи, арабы и многие другие народы Ближнего Востока имели такие же системы счисления.

При ее помощи можно было просто записать числа до ста миллионов (100 000 000). Эта система по быстроте счета мало отличается от «арабской». И хоть она не позиционная, но в ней есть мультипликативность.

3.5 Славянская глаголическая десятеричная

Эта система была создана для обозначения чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. По организации она в точности повторяет греческую нумерацию. Использовалась она с VIII по XIII в.

1	10	100	1 000
2	20	200
3	30	300
4	40	400
5	50	500
6	60	600
7	70	700
8	80	800
9	90	900

Числа записывали из цифр так же слева, направо, от больших к меньшим цифрам. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали. Такая запись числа аддитивная, то есть в ней используется только сложение:

= 800+60+3 = 863

Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, или точки.

3.6 Славянская кириллическая десятеричная алфавитная

Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком:

Читаем дословно "четырнадцать" - "четыре и десять". Как слышим, так и пишем: не 10+4, а 4+10, - четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.

Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение:

= 800+60+3

Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.

Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:

	Тысяча	1000
	Тьма	10 000
	Легион	100 000
	Леодр	1 000 000
	Ворон	10 000 000
	Колода	100 000 000

Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.

3.7 Древнеиндийские системы счисления

Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.

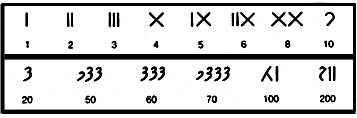
Наряду с этой системой существовала в Индии еще одна система счисления брахми.

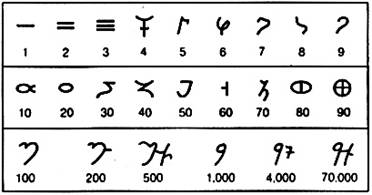
Числа брахми записывались слева направо. Однако в обеих системах было не мало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми, было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы.

В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света». Например, число 2441 произносилось так: глаза океанов стороны света луны.

3.8 Недостатки непозиционной системы счисления

Непозиционные системы счисления имеют ряд существенных недостатков:

1. Существует постоянная потребность введения новых знаков для записи больших чисел.

2. Невозможно представлять дробные и отрицательные числа.

3. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов.

Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.

Далее рассмотрим позиционные системы счисления.

4 Позиционные системы счисления

4.1 Вавилонская десятеричная / шестидесятеричная

В древнем Вавилоне примерно во II тысячелетие до нашей эры была такая система счисления - числа менее 60 обозначались с помощью двух знаков: для единицы, и для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например

- 3; - 20; - 32; - 59

Числа больше 60 записывались по разрядам, с небольшими пробелами между ними:

Так записывается число 302, то есть 5*60+2.

1*60*60+2*60+5 = 3725

А это 1*60*60+2*60+5 = 3725.

Но представление не которых чисел в этой системе будет одинаковым, например, число 302, может быть и равно и 5*60*60 + 2 = 18002. Так как нет значка для обозначения нуля.

Лишь в V веке до нашей эры был введен особый знак - наклонный клин для обозначения пропущенных разрядов, игравший роль нуля.

2*60*60+3 = 7203

это запись числа 7203 (2*60*60+3).

Однако отсутствие низшего разряда не обозначалось, и поэтому число 180 = 3*60 записывалось так , а обозначать эта запись могла и 3, и 180, и 10800 (3*60*60), и т. д.

Считается, что десятичная система была у шумеров, а после того как их завоевали семиты, их система была приспособлена под шестидесятеричную систему семитов.

Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби применяются до сих пор при измерении времени. Например, одна минута = 60 секунд, один час = 60 минут.

4.2 Древнекитайская десятеричная

Эта система одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае.

1		6
2		7
3		8
4		9
5	O	0

Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок - аналог нашего нуля). Чтобы не перепутать разряды использовали несколько служебных иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде.


10	100	1 000	10 000

одна тысяча - 1*1 000 = 1000;

пять сотен четыре десятка восемь - 5 * 100+4* 10+8 = 548

Эта мультипликативная запись, так как в ней используется умножение. Она десятичная, в ней есть знак нуля, кроме этого она позиционная. Т.е. она почти соответствует «арабской» системе счисления.

4.3 Двадцатеричная система счисления индейцев Майя или долгий счет

Эта система очень интересна тем, что на ее развитие не повлияла ни одна из цивилизаций Европы и Азии. Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Основанием этой системы было число 20, хотя сильно заметны следы пятеричной системы. Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять).

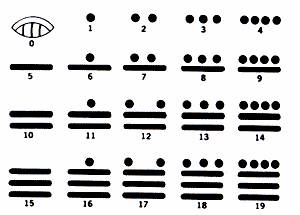
Число 20 изображалось из двух цифр, ноль и один наверху и называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие, в результате получалась «этажерка» с полками. Если число ноль появлялось без единицы наверху, то это обозначало, что единиц данного разряда нет. Но, если хоть одна единица была в этом разряде, то знак нуля исчезал, например, число 21, это будет . Так же в нашей системе счисления: 10 – с нулем, 11 – без него. Вот несколько примеров чисел:

В двадцатеричной системе счета древних майя есть исключение: стоит прибавить к числу 359 только одну единицу первого порядка, как это исключение немедленно вступает в силу. Суть его сводится к следующему: 360 является начальным числом третьего порядка и его место уже не на второй, а на третьей полке.

Но тогда выходит, что начальное число третьего порядка больше начального числа второго не в двадцать раз (20x20=400, а не 360!), а только в восемнадцать! Значит, принцип двадцатеричности нарушен! Все верно. Это и есть исключение.

Дело в том, что у индейцев Майя 20 дней-кинов образовывали месяц или уинал. 18 месяцев-уиналов образовывали год или туну (360 дней в году) и так далее:

        К'ин = 1 день.
        Виналь = 20 к'ин = 20 дней.
        Тун = 18 виналь = 360 дней = около 1 года.
        К'атун = 20 тун = 7200 дней = около 20 лет.
        Бак'тун = 20 к'атун = 144000 дней = около 400 лет.
        Пиктун = 20 бак'тун = 2880000 дней = около 8000 лет.
        Калабтун = 20 пиктун = 57 600 000 дней = около 160000 лет.
        К'инчильтун = 20 калабтун = 1152000000 дней = около 3200000 лет.
        Алавтун = 20 к'инчильтун = 23040000000 дней = около 64000000 лет.

Это довольно сложная система счисления, в основном использовалась жрецами для астрономических наблюдений, другая система индейцев Майя была аддитивной, похожей на египетскую и применялась в повседневной жизни.

5 История «арабских» чисел.

История наших привычных «арабских» чисел очень запутана. Нельзя сказать точно и достоверно как они произошли. Вот один из вариантов этого истории этого происхождения. Одно точно известно, что именно благодаря древним астрономам, а именно их точным расчетам мы и имеем наши числа.

Как мы уже знаем, в вавилонской системе счисления присутствует знак для обозначения пропущенных разрядов. Примерно во II веке до н.э. с астрономическими наблюдениями вавилонян познакомились греческие астрономы (например, Клавдий Птолемей). Они переняли их позиционную систему счисления, но целые числа они записывали не с помощью клиньев, а в своей алфавитной нумерации, а дроби в вавилонской шестидесятеричной системой счисления. Но для обозначения нулевого значения разряда греческие астрономы стали использовать символ "0" (первая буква греческого слова Ouden - ничто).

Между II и VI веками н.э. индийские астрономы познакомились с греческой астрономией. Они переняли шестидесятеричную систему и круглый греческий нуль. Индийцы соединили принципы греческой нумерации с десятичной мультипликативной системой взятой из Китая. Так же они стали обозначать цифры одним знаком, как было принято в древнеиндийской нумерации брахми. Это и был завершающий шаг в создании позиционной десятичной системы счисления.

Блестящая работа индийских математиков была воспринята арабскими математиками и Аль-Хорезми в IX веке написал книгу "Индийское искусство счета", в которой описывает десятичную позиционную систему счисления. Простые и удобные правила сложения и вычитания сколь угодно больших чисел, записанных в позиционной системе, сделали ее особенно популярной в среде европейских купцов.

В XII в. Хуан из Севильи перевел на латынь книгу "Индийское искусство счета", и индийская система счета широко распространилась по всей Европе. А так как труд Аль-Хорезми был написан арабском языке, то за индийской нумерацией в Европе закрепилось неправильное название - "арабская". Но сами арабы именуют цифры индийскими, а арифметику, основанную на десятичной системе - индийским счетом.

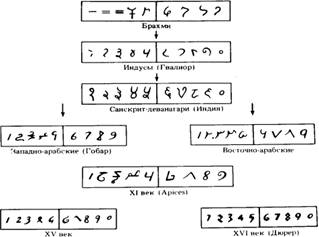Форма «арабских» цифр со временем сильно изменялась. Та форма, в которой мы их пишем, установилась в XVI веке.

Даже Пушкин предложил свой вариант формы арабских чисел. Он решил, что все десять арабских цифр, включая нуль, помещаются в магическом квадрате.

6 История нуля.

Нуль бывает разный. Во-первых, нуль – это цифра, которая используется для обозначения пустого разряда; во-вторых, нуль – это необычное число, так как на нуль делить нельзя и при умножении на нуль любое число становиться нулем; в-третьих, нуль нужен для вычитания и сложения, иначе, сколько будет, если из 5 вычесть 5?

Впервые нуль появился в древневавилонской системе счисления, он использовался для обозначения пропущенных разрядов в числах, но такие числа как 1 и 60 у них записывали одинаково, так как нуль в конце числа у них не ставился. В их системе нуль выполнял роль пробела в тексте.

Изобретателем формы нуля можно считать великого греческого астронома Птолемея, так как в его текстах на месте знака пробела стоит греческая буква омикрон, очень напоминающая современный знак нуля. Но Птолемей использует нуль в том же смысле, что и вавилоняне.

На стенной надписи в Индии в IX веке н.э. впервые символ нуля встречается в конце числа. Это первое общепринятое обозначение современного знака нуля. Именно индийские математики изобрели нуль во всех его трех смыслах. Например, индийский математик Брахмагупта еще в VII века н.э. активно стал использовать отрицательные числа и действия с нулем. Но он утверждал, что число, деленное на нуль, есть нуль, что конечно ошибка, но настоящая математическая дерзость, которая привела к другому замечательному открытию индийских математиков. И в XII веке другой индийский математик Бхаскара делает еще попытку понять, что же будет при делении на нуль. Он пишет: "количество, деленное на нуль, становится дробью, знаменатель которой равен нулю. Эту дробь называют бесконечностью".

Леонардо Фибоначчи, в своем сочинении "Liber abaci" (1202) называет знак 0 по-арабски zephirum. Слово zephirum – это арабское слово as-sifr, которое произошло от индийского слова sunya, т. е. пустое, служившего названием нуля. От слова zephirum произошло французское слово zero (нуль) и итальянское слово zero. С другой стороны, от арабского слова as-sifr произошло русское слово цифра. Вплоть до середины XVII века это слово употреблялось специально для обозначения нуля. Латинское слово nullus (никакой) вошло в обиход для обозначения нуля в XVI веке.

Нуль - это уникальный знак. Нуль – это чисто абстрактное понятие, одно из величайших достижений человека. Его нет в природе окружающей нас. Без нуля можно спокойно обойтись в устном счете, но невозможно обойтись для точной записи чисел. Кроме этого, нуль находится в противовесе всем остальным числам, и символизирует собой бесконечный мир. И если “все есть число”, то ничто есть все!

Заключение

В этой работе были рассмотрены 11 древних систем счисления, история «арабских» чисел и нуля. Из всех рассмотренных систем счисления, наиболее интересной мне показалась древне китайская нумерация. Так как она наиболее близка к нашей «арабской» системе счисления. Наиболее красивые цифры и числа в древнеегипетской системе счисления. Так же мне удалось узнать запутанную историю происхождения «арабских» чисел и нуля.

В продолжение этой работы хотелось бы, исследовать каким образом в древности вели устный счет (сложение, вычитание, умножение и деление), а также как использовались счетные доски (например, греческий абак). Кроме этого, интересно узнать, как с помощью древних цифр происходило представление дробей. Можно попробовать создать свою систему счисления (двенадцатеричную).

Список использованной литературы

1. В. Лёвшин, Три дня в Карликании, 1966

2. Всевозможные нумерации и системы счисления (http://www.megalink.ru/~agb/n/numerat.htm)

3. А.П.Юшкевич, История математики, Том 1, 1970

4. Г. И. Глейзер, История математики в школе, 1964

5. И. Я. Депман, История арифметики, 1965

6. А.Костинский, В.Губайловский, Триединый нуль (http://www.svoboda.org/programs/sc/2004/sc.011304.asp)

7. Кузьмищев В. А. Тайна жрецов майя. 2-е изд. — М., «Молодая гвардия», 1975